
Exploring Tangent Circles
by
Laura Kimbel
In this exercise, I will explore the construction of a circle that is tangent to 2 other circles. I began by drawing 2 circles. Then, in order to locate the center of our tangent circle, I had to construct an isosceles triangle. CLICK HERE for a GSP sketch on the construction.
Now, I will examine what happens to the center of our tangent circle, as we move one of our tangent points. By constructing the Locus of the center of the tangent circle, we can see the path that it travels as we drag one of our tangent points around Circle 1. Below is an analysis of the different situations we could construct and how it affects the locus of the center of our tangent circle.
LOCUS OF CENTER OF TANGENT CIRCLE
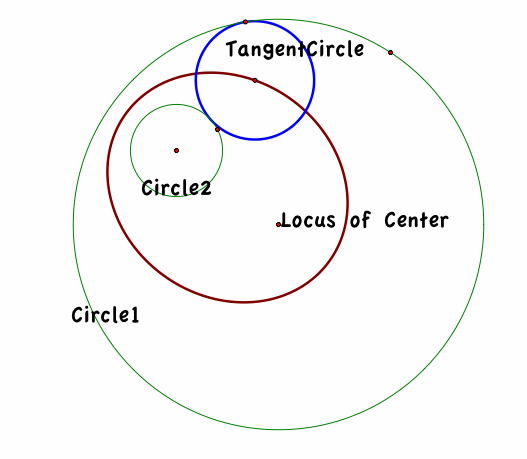
Circle 2 is inside Circle 1. Locus of points as we trace the center of our Tangent Circle creates an ellipse.
What if circle 2 is inside Circle 1 but tangent to Circle 2?
We can see that we still have an ellipse for our Locus, yet there is also a point of tangency to Circle 1 and Circle 2.
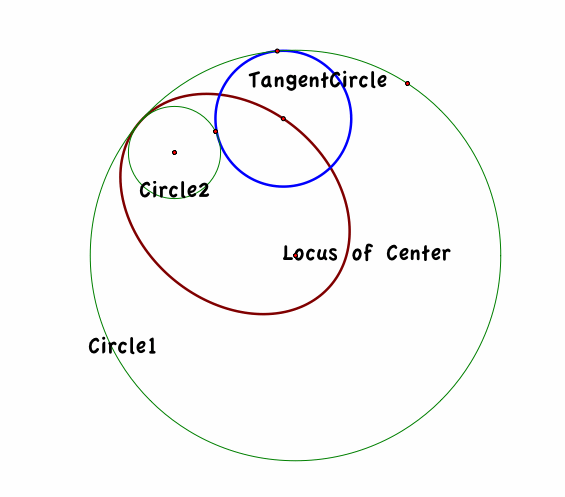
What if Circle 2 intersects Circle 1 in 2 points?
We still have an ellipse, but this time, part of the ellipse is inside Circle 1 and part is outside Circle 1.
What if Circle 2 is outside of Circle 1, but tangent at a point?
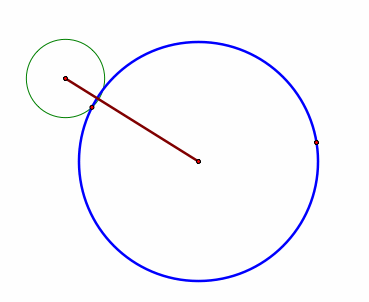
We can see that the Locus becomes a line segment between the 2 centers of the circles, and that tangent circle now coincides with our larger circle.
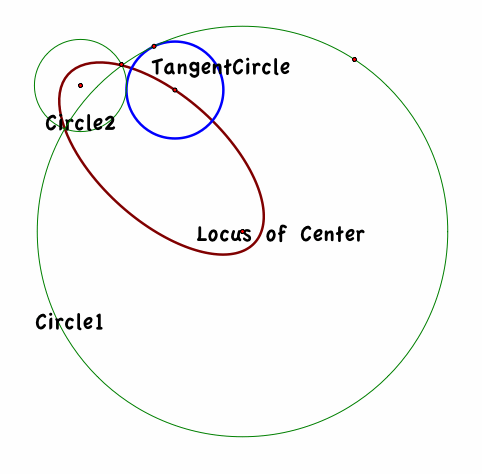
What if Circle 2 lies completely outside of Circle 1?
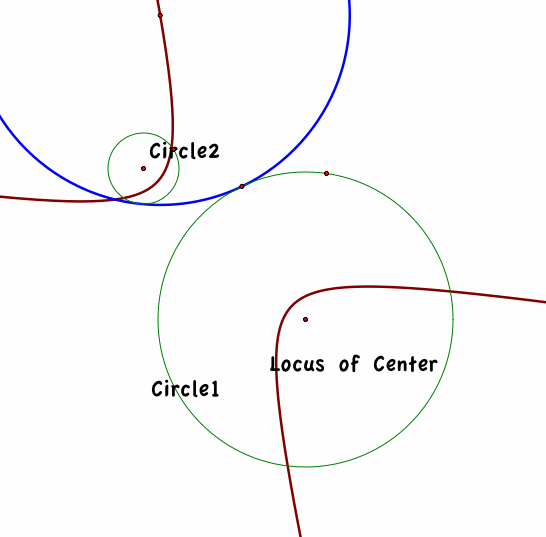
Now, as we move circle 2 completely outside of Circle 1, our Locus shifts to a hyperbola.
CLICK HERE to view a GSP sketch. Change the sizes and locations of the circles to observe how it affects the Locus of the Center of our tangent circle, like I did above.
Observations:
As we moved Circle 2 around, our Locus resembled different types of conics. It started out as an ellipse when 1 circle was inside of the other circle. Even if Circle 1 was tangent to Circle 2 or in the case where Circle 2 intersected Circle 1 at 2 points, as long as at least part of Circle 2 was inside Circle 1, an ellipse was formed. We were also able to produce a hyperbola when we moved Circle 2 completely outside of Circle 1.
Another interesting part was when the Locus was a line segment between the the 2 centers.
When would the Locus be a circle?
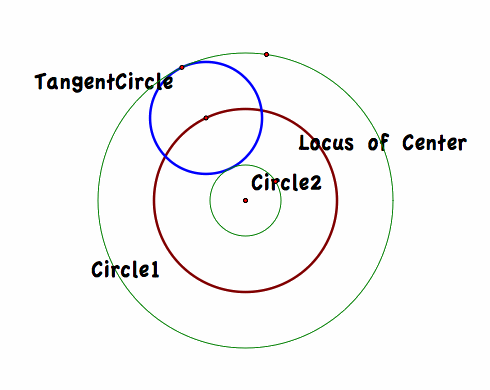
Another way to view the locus of the center of our tangent circle is by viewing the locus of the lines tangent to our resulting ellipses or hyperbola:



